全国2006年4月高等教育自学考试《高等数学(工本)》试题
《自考视频课程》名师讲解,轻松易懂,助您轻松上岸!低至199元/科!
本试卷总分100分,考试时间150分钟。
一、单项选择题(每小题2分,共40分)
1.函数f(x)=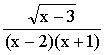 的连续区间是( )
的连续区间是( )
A.(-∞,-1)∪(-1,2)∪(2,+∞)
B.(-∞,-2)∪(1,+∞)
C.(-∞,-1)∪(2,+∞)
D.[3,+∞]
2.下列函数在其定义域内为有界函数的是( )
A.
B.
C.
D.
3.极限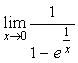 ( )
( )
A.等于0
B.等于1
C.为无穷大
D.不存在,但不是无穷大
4.曲线y=1+sinx在点(![]() )处的切线方程为( )
)处的切线方程为( )
A.
B.
C.
D.
8.设二阶可导函数f(x)在x0点满足f′(x0) =0,f〞(x0)>0,则x0是f(x)的( )
A.驻点
B.零点
C.极大值点
D.非极值点
6.设参数方程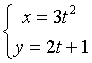 确定了函数y=y(x),则
确定了函数y=y(x),则![]() =( )
=( )
A.
B.
C.
D.
15.设函数f(x,y)=![]() ,则点(0,0)是f(x,y)的( )
,则点(0,0)是f(x,y)的( )
A.驻点
B.极小值点
C.极大值点
D.非极值点
5.设函数f(x)=cos![]() ,则
,则![]() =( )
=( )
A.
B.
C.
D.
16.设积分区域G:x^2+y^2+z^2≤R^2,则三重积分![]() 在柱面坐标下的累积分为 ( )
在柱面坐标下的累积分为 ( )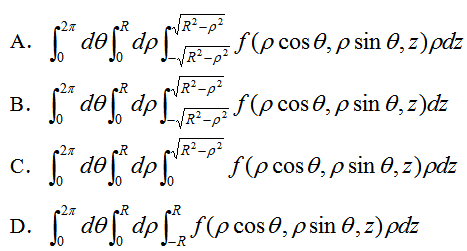
A.
B.
C.
D.
17.无穷级数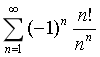 是( )
是( )
A.条件收敛
B.绝对收敛
C.发散
D.敛散性不确定的
18.幂级数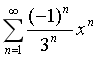 在(-3,3)内的和函数S(x)=( )
在(-3,3)内的和函数S(x)=( )
A.
B.
C.
D.
19.微分方程(![]() )^2+3
)^2+3![]() -x^2=1的阶数是( )
-x^2=1的阶数是( )
A.1
B.2
C.3
D.4
20.微分方程y〞-3y′=0满足y(0)=0, y′(0)=1的特解为( )
A.
B.
C.
D.
10.不定积分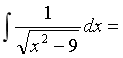 ( )
( )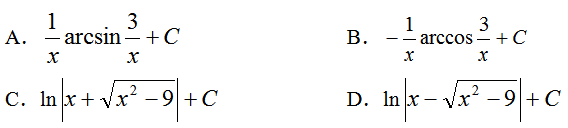
A.
B.
C.
D.
7.设函数f(x)=![]() ,则函数f(x)在x=0.01,△x=-0.1处的微分df(x)=( )
,则函数f(x)在x=0.01,△x=-0.1处的微分df(x)=( )
A.-1
B.-0.5
C.-0.001
D.0.001
11.设f(x)在[a,b]上连续,当x∈[a,b]时,则f(x)的一个原函数为( )
A.
B.
C.
D.
9.曲线y=![]() -12x+36的凹向区间为( )
-12x+36的凹向区间为( )
A.(-∞,8]
B.[8,+∞)
C.(-∞,4]∪[12,+∞)
D.(-∞,+∞)
12.点(-3,1,-5)在( )
A.第四卦限
B.第五卦限
C.第六卦限
D.第七卦限
13.过点(1,-3,-2)并且垂直于平面x-3y+2z-7=0的直线方程为( )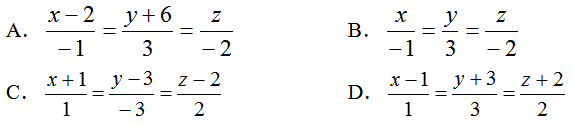
A.
B.
C.
D.
14.已知方程y-ln![]() =0确定函数z=z(x,y),则
=0确定函数z=z(x,y),则![]() =( )
=( )
A.
B.
C.
D.
二、填空题(每小题2分,共20分)
1.设函数f(2x)=![]() ,g(x)=x-4,则f(g(2))=_________.
,g(x)=x-4,则f(g(2))=_________.
3.曲线y=(x-1)^3-1的拐点坐标为_____.
5.函数f(x)=arctgx在[-1,1]上的平均值为______.
2.极限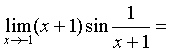 _______.
_______.
7.设函数f(x,y)=![]() ,则df(x,y)=___________.
,则df(x,y)=___________.
4.不定积分![]() =_______.
=_______.
10.微分方程xdx+ydy=0的通解为_______.
6.点P(2,-1,3)到平面x+y-z+1=0的距离为_____.
8.设积分区域B:1≤x^2+y^2≤3,则二重积分![]() =_______.
=_______.
9.函数f(x)=![]() 展开成x的幂级数为______.
展开成x的幂级数为______.
三、计算题(每小题5分,共25分)
1.求极限![]()
2.设函数f(x)=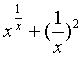 (x>0),求f′(x).
(x>0),求f′(x).
4.已知函数f(x)为连续函数,并且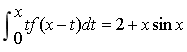 求
求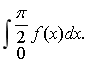
3.求不定积分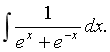
5.将函数f(x)=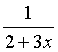 展开为x-1的幂级数.
展开为x-1的幂级数.
四、应用和证明题(每小题5分,共15分)
1.对任意的实数x1和x2,证明有不等式 ![]() 成立.
成立.
2.求由曲线y^2=x,2y^2=x及x=1所围平面图形的面积.
3.求椭球面x^2+2y^2+3z^2=6上点(1,1,1)处的法线方程.
本文标签:江西自考 高等数学(工本) 全国2006年4月高等教育自学考试《高等数学(工本)》试题
转载请注明:文章转载自(http://www.zikao.jx.cn)
⊙小编提示:添加【江西自考网】招生老师微信,即可了解2024年江西自考政策资讯、自考报名流程、准考证打印方法、成绩查询时间以及领取历年真题资料、个人专属备考方案等相关信息!

(添加“江西自考网”招生老师微信,在线咨询报名报考等相关问题)
填写下方信息,立即领取江西自考《备考方案》!

微信扫码添加
《江西自考网》免责声明:
1、由于各方面情况的调整与变化,本网提供的考试信息仅供参考,考试信息以省考试院及院校官方发布的信息为准。
2、本网信息来源为其他媒体的稿件转载,免费转载出于非商业性学习目的,版权归原作者所有,如有内容与版权问题等请与本站联系。联系邮箱:812379481@qq.com



 ×
×




















